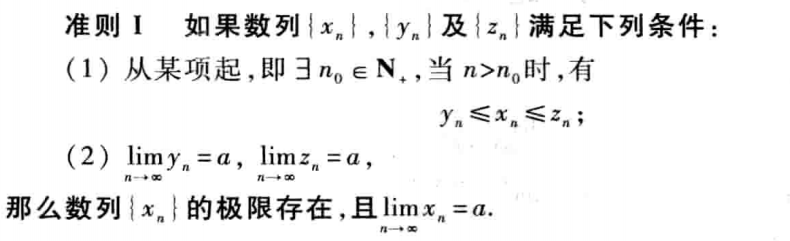同济版《高等数学第七版》对该极限有如下证明：

而夹逼定理为下面的两个准则：


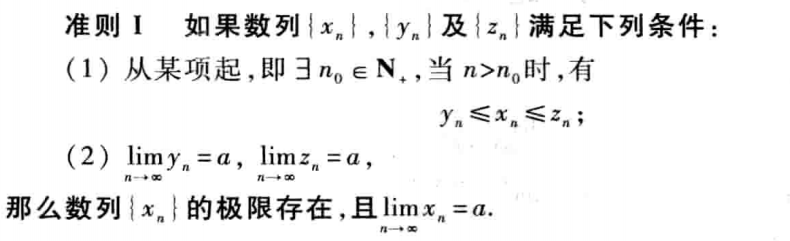
根据以上两个准则对照书中的证明不难发现，书中证明中的夹逼定理运用情况并不与上面的两个准则十分相符，在证明中，更像是两个数列夹着一个函数，而准则中并没有指出两个数列夹着一个函数有所谓夹逼定理。那么这里究竟是如何运用夹逼定理的呢？

事实上，“设n<=x<n+1”就已经说明了证明中的看似数列的部分并非数列，而是特殊的函数，也就是说，这个n与自变量x相关，这使得不等式左右两边看似为数列的两个式子并不是完全是我们平时所理解的数列。这个n是[x]，也就是对x取整后的值，是实数x的函数而不是平时我们定义数列时所认为的正整数(虽然它们的取值都一样)。

所以或许用下面的表达方式更容易理解为什么这里能够运用夹逼定理：
lim⁡x→∞exp⁡(−x)=0\lim_{x \to \infty} \exp(-x) = 0

设n=[x]，则n<=x<n+1，故[1+12]n[1+\frac{1}{2}]^n<[1+1x]x[1+\frac{1}{x}]^x<[1+1n](n+1)[1+\frac{1}{n}]^(n+1)，即[1+1[x]+1][x][1+\frac{1}{[x]+1}]^[x]<(1+1x)x(1+\frac{1}{x})^x<[1+1[x]]([x]+1)[1+\frac{1}{[x]}]^([x]+1)，

设函数g(x)=[1+1([x]+1)][x][1+\frac{1}{([x]+1)}]^[x]，函数h(x)=[1+1[x]]([x]+1)[1+\frac{1}{[x]}]^([x]+1)，则

lim⁡x→∞g(x)\lim_{x \to \infty} g(x) =lim⁡x→∞[1+1([x]+1)][x]\lim_{x \to \infty} [1+\frac{1}{([x]+1)}]^[x] ，因n=[x]，则当x→∞{x \to \infty}，n→∞{n \to \infty}，故运用复合函数的极限运算法则知，

lim⁡x→∞g(x)\lim_{x \to \infty} g(x) = lim⁡x→∞[1+1([x]+1)][x]\lim_{x \to \infty} [1+\frac{1}{([x]+1)}]^[x]=lim⁡n→∞[1+1(n+1)]n\lim_{n \to \infty} [1+\frac{1}{(n+1)}]^n =e

同理有
lim⁡x→∞h(x)\lim_{x \to \infty} h(x) = lim⁡x→∞[1+1[x]]([x]+1)\lim_{x \to \infty} [1+\frac{1}{[x]}]^([x]+1) = lim⁡n→∞[1+1n](n+1)\lim_{n \to \infty} [1+\frac{1}{n}]^(n+1) = e，

故由准则I`知，lim⁡x→∞[1+1x]x\lim_{x \to \infty} [1+\frac{1}{x}]^x = e.